Chapter 1: Answers 4 Jack K. Cohen Colorado School of Mines

1. r 50, 008.33. A real pitfall here is getting trapped into investigating the regime where r < s = 1000—``obviously'' the radius of the asteroid would sensibly be much larger than s. By the way, the word ``obviously'' in mathematics means ``clear when you think about it for awhile''. For example, some real smart people have been known to have put up a first Plot for values of r near 0 in solving the present problem.

   Another problem is that we have no idea where to hunt for the ``physically sensible'' root. As promised in the problem statement, we will develop methods for this in a few weeks.

2. (1.2.24) A sketch reveals some nice right triangles: d = .

3. It checks.

4. No solution given to honor problems.

5. (1.2.25) d = .

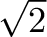
6. 1. It checks (despite the answer in the back of the book).
   2. The form y = mx + b₁, y = mx + b₂ doesn't include the case of two vertical lines.

7. 1. y = 3x - 2.

   2. y = 2.1x - 1.1.

   3. y = 2.01x - 1.01.

   4. Slope is m = 2, tangent line is y = 2x - 1.

   5. Did you notice that the curve for y = x² was almost linear in the ``zoomed'' plot?

   6. The precise definition requires calculus concepts that will be discussed soon. (Attempts to give a definition in terms of only algebra and geometry concepts are sure to be inadequate.) It is a secant line.